Если данные анализа не отображаются или отображаются некорректно

В случае, если при выводе результатов рассчётов возникают ошибки или зависание, вставьте данные без названий и повторите анализ заново

Выбор подходящего коэффициента корреляции

Коэффициент корреляции Пирсона имеет ряд требований, которые необходимо выполнить для получения высокой точности расчётов.

Условия использования коэффициента корреляции Пирсона:


• 1. Переменные Х и Y должны иметь нормальное распределние.
• 2. Характер связи между переменными должен быть линейным.
• 3. Наблюдения обязательно должны быть парными, т.е., количество значений Х должно равняться количеству значений Y.
• 4. Для наиболее высокой точности расчёта корреляции Пирсона количество наблюдений должно превышать 25.

Коэффициент корреляции Спирмена, в отличие от коэффициента Пирсона, менее требователен к исходным данным. Так, например, для его расчёта не требуется подчинение выборок закону нормального распределения.

Для использования коэффициента корреляции Спирмена должны быть соблюдены следующие условия:


• 1. Данные одной из выборок могут быть представлены в порядковой шкале, однако, вторая выборка должна быть представлена количественными данными.
• 2. Количество наблюдений должно быть не менее 5.
• 3. Для более точного расчёта коэффициента корреляции Спирмена желательно, чтобы внутри выборок не было совпадающих значений.

Правильный ввод данных

Ручной ввод

При ручном вводе данных числа, расположенные по горизонтали, необходимо разделять точкой с запятой (;). На конце строки точка с запятой не нужна (рисунок 1).

Рисунок 1

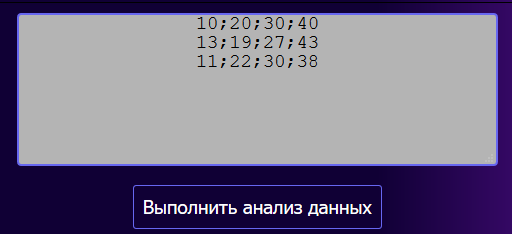
Копирование данных из Excel

Для корректной работы калькулятора коэффициентов корреляциии необходимо, чтобы названия рядов данных в первой строке или столбце были без переносов, допустимы только пробелы. В качестве исходных данных допустимо использование как непосредственно экспериментальных значений в виде повторностей, так и средних. Однако, для более точного расчёта коэффициентов корреляции лучше использовать экспериментальные данные без расчёта средних значений, поскольку с ростом количества наблюдений растёт точность расчёта коэффициентов корреляции. Правильным вариантом представления данных будет разбиение по повторностям (рисунок 2).

Рисунок 2

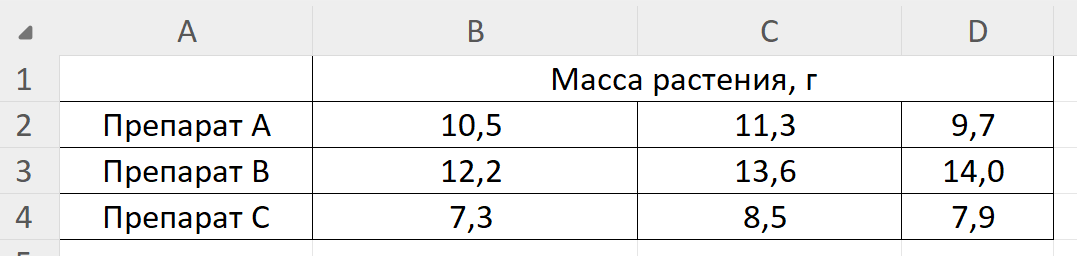
Для начала анализа необходимо выделить данные, как показано на рисунке 3, и скопировать их в поле ввода.

Рисунок 3

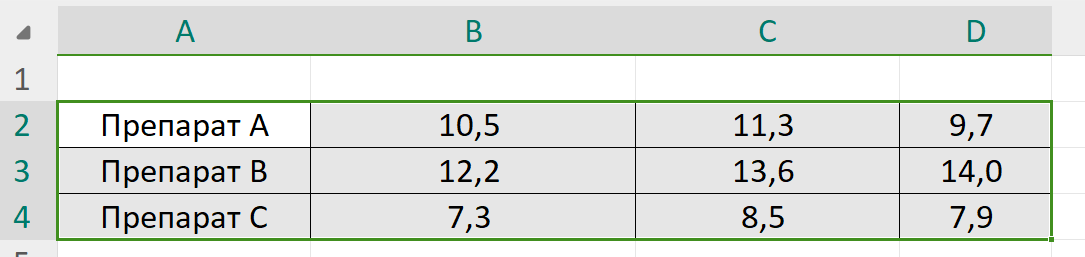
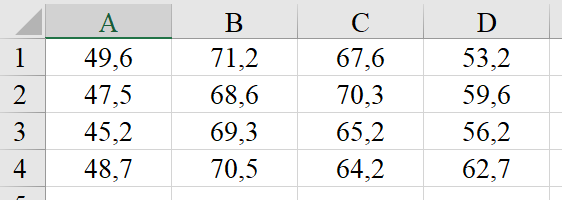
В представленном примере на рисунке 3 повторности расположены слева-направо и есть названия вариантов в первом столбце. Соответствующие пункты меню нужно выбрать перед проведением анализа. После того, как исходные данные вставлены в поле ввода, жмём кнопку Выполнить анализ данных и ждём результата. В следующем примере на рисунке 4 показан вариант размещения данных, когда повторности расположены сверху-вниз и есть названия вариантов в первой строке.

Рисунок 4

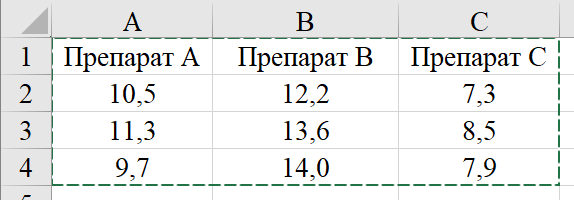
Также возможен анализ данных и без названий (рисунок 5). При этом необходимо правильно выбрать вариант группировки для корректного сравнения значений (по столбцам – "Повторности расположены сверху-вниз" или по строкам таблицы – "Повторности расположены слева-направо").

Рисунок 5